Day 1 - Graphing & Function

Graphing

The Cartesian coordinate system is a tool that shows the relationship between two variables. It does this by pairing numbers that make an equation true simultaneously or by illustrating relationships between two quantities—one on the horizontal axis (x) and the other on the vertical axis (y).

Tips for Interpreting Graphs

When analyzing a graph, focus on each dimension individually:

• Horizontal axis (x): Understand what the x-coordinates represent.

• Vertical axis (y): Analyze what the y-coordinates signify.

As you progress, you’ll learn to recognize equations and anticipate what their graphs should look like.

Example: Plotting Points

Consider the equation: \(y=2x+1\)

To graph this, calculate several ordered pairs \((x, y)\):

x	y
-2	-3
-1	-1
0	1
1	3
2	5

Plot these points on the Cartesian coordinate system and connect them to form a straight line.

---

Functions

A function is a relation in which no input value (x) is paired with more than one output value (y).

Functions can be represented in three ways: 1. A set of ordered pairs Example: \({(1, 2), (2, 4), (3, 6)}\) 2. A graph Example: The graph of \(y=2x\) is a straight line through the origin. 3. An equation Example: \(y=x^2\).

Key Components of a Function

• Domain: The set of all possible input values x-coordinates. Example: For \(f(x) = \sqrt{x}\), the domain is \([0, \infty)\) since negative inputs are undefined for square roots.
• Range: The set of all possible output values y-coordinates. Example: For \(f(x) = x^2\), the range is \([0, \infty)\).

Note on Interval Notation

• [a, b]: Closed interval (includes endpoints).
• (a, b): Open interval (excludes endpoints).

---

Linear Equations

Forms of Linear Equations

1. Standard Form: \[ax + by + c = 0\] Constants \(a\), \(b\) and \(c\), where \(a\) and \(b\) are not both zero.

2. Slope-Intercept Form: \[y = mx + b\]

   • \(m\): Slope of the line.
   • \(b\): y-intercept (where the line crosses the y-axis).

3. Point-Slope Form: \[y - y_1 = m(x - x_1)\]

   • \(m\): Slope of the line.
   • \((x_1, y_1)\): A point on the line.

Notes on Slopes

• Parallel lines have equal slopes \(m_1 = m_2\).
• Perpendicular lines have slopes that are opposite reciprocals \(m_1 \cdot m_2 = -1\).

Example: Perpendicular lines

If \(y = 2x + 3\), the line perpendicular to it would have slope \(-\frac{1}{2}\), e.g., \(y = -\frac{1}{2}x + 1\).

---

Non-Linear Equations

Examples of non-linear equations include:

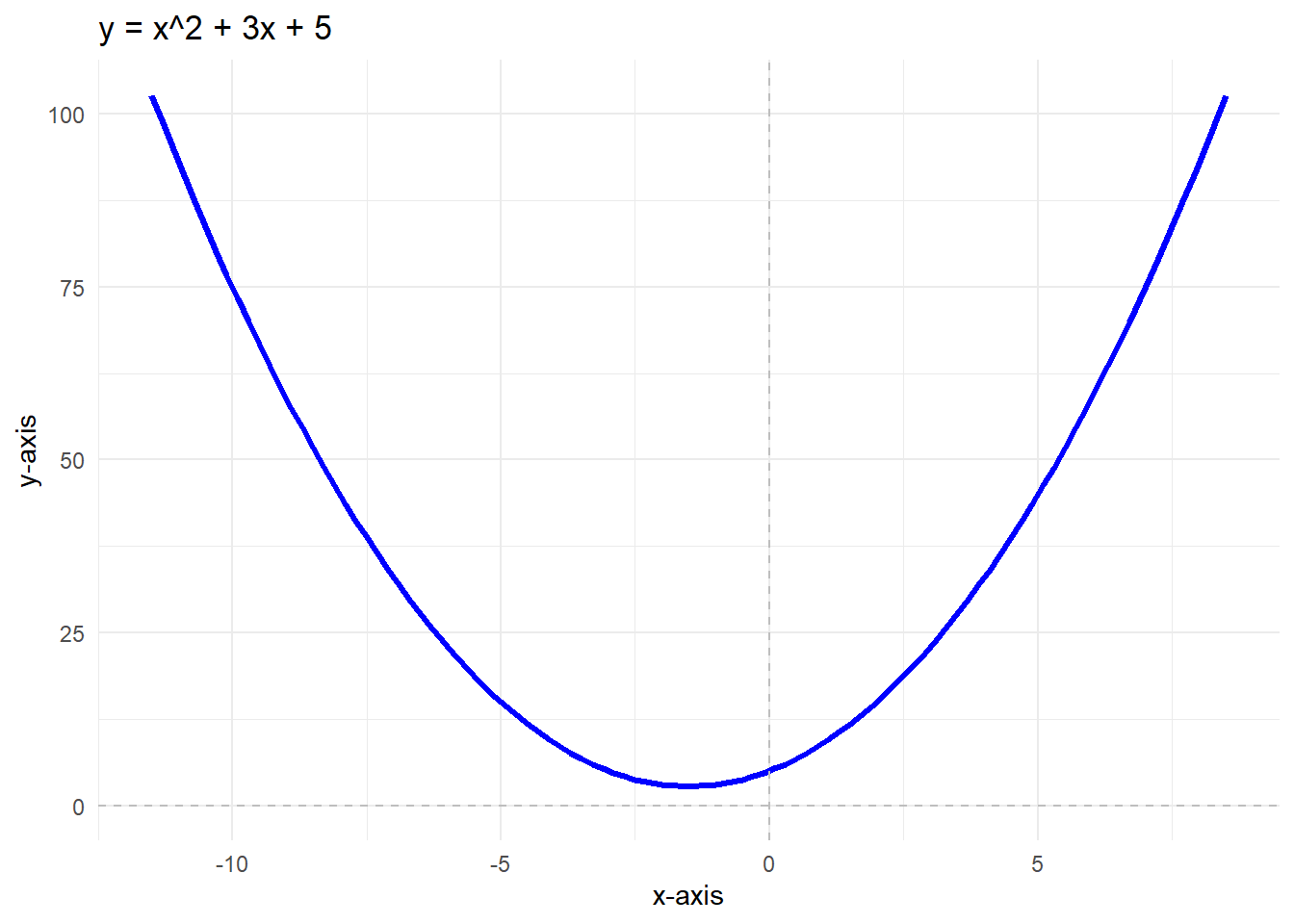
• Quadratic equations: \(y = ax^2 + bx + c\)

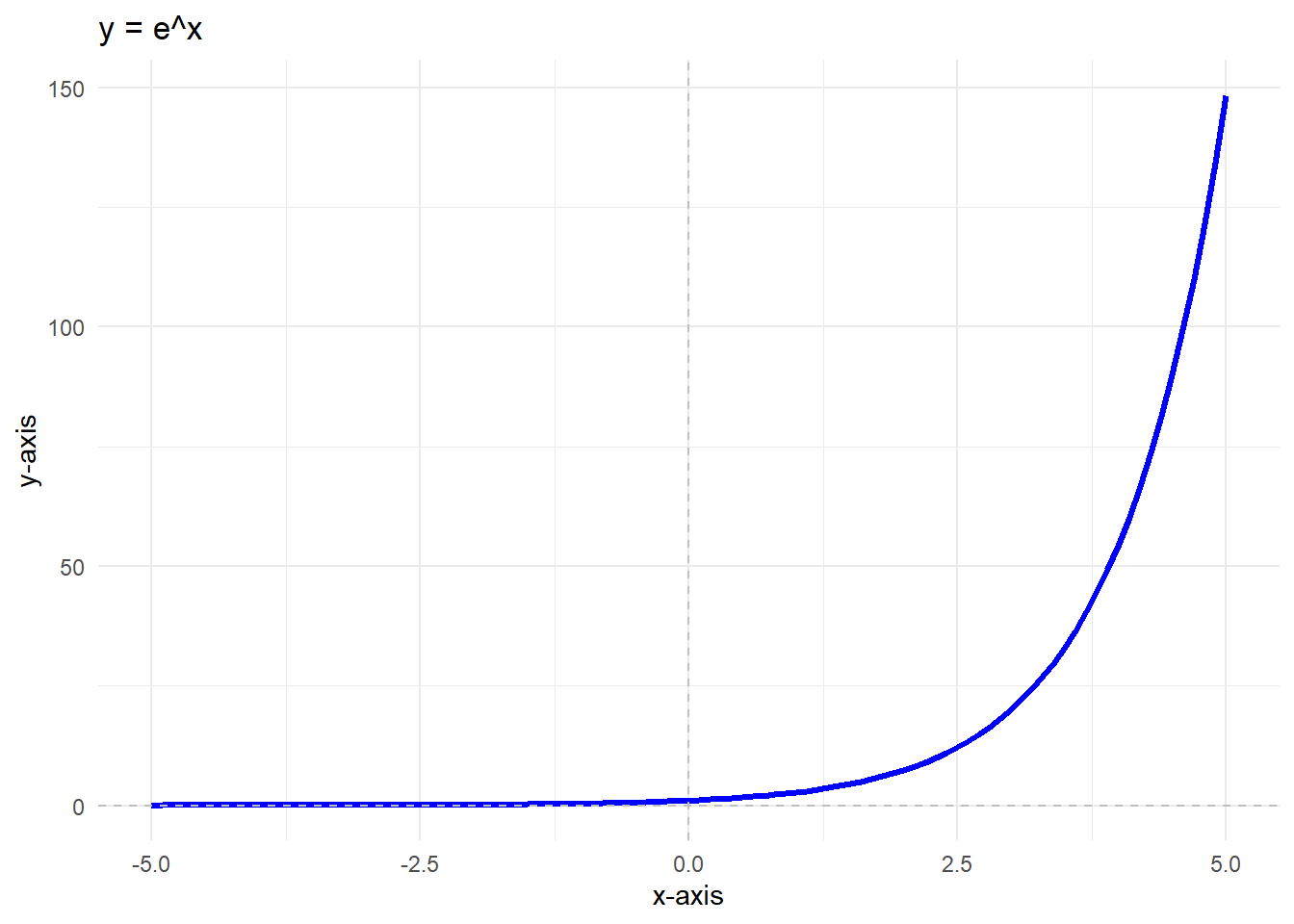
• Exponential functions: \(y = e^x\)

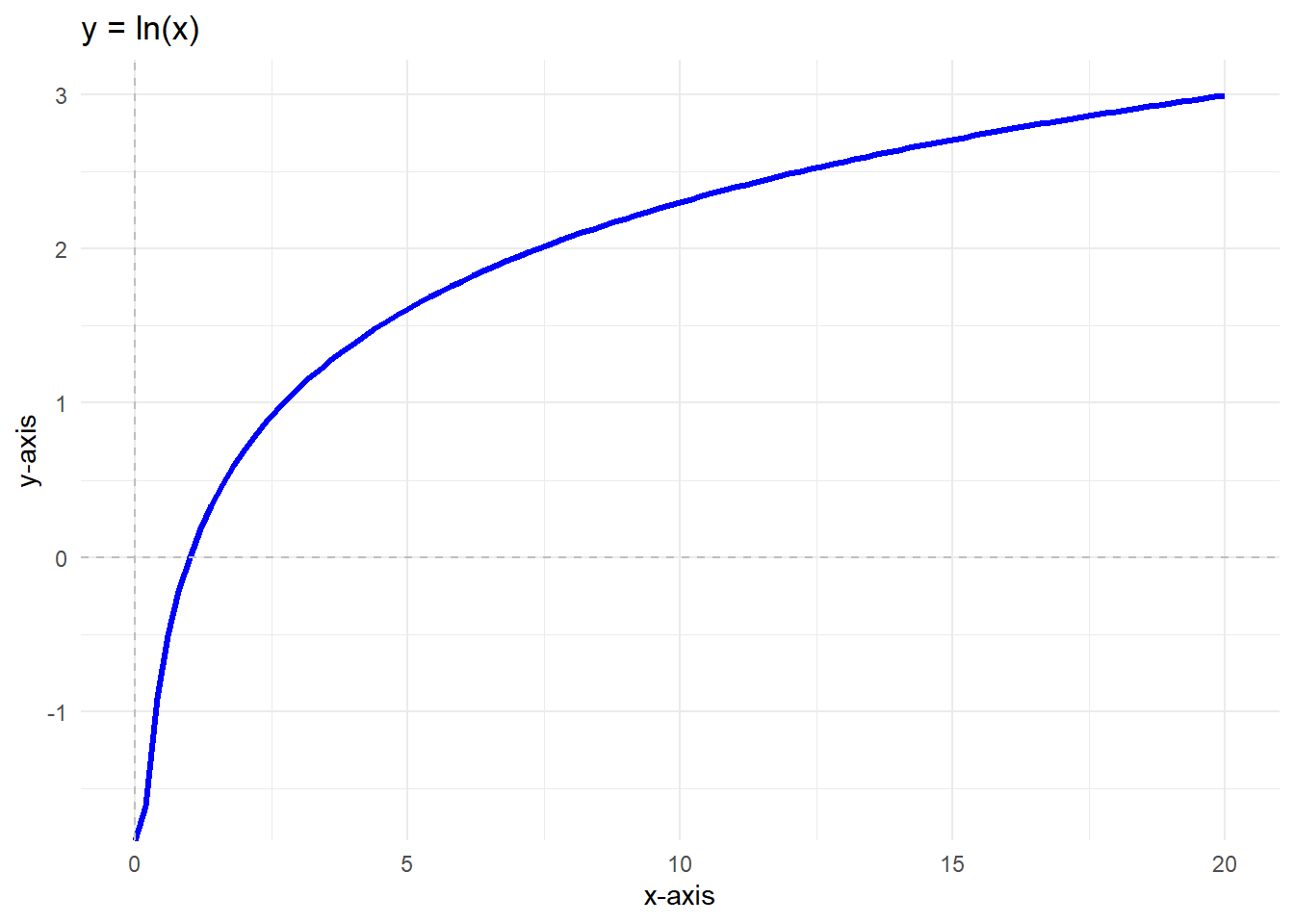
• Logarithmic functions: \(y = \ln(x)\)

Each has distinct graph shapes and requires different approaches to analysis.

---

Systems of Equations

A system of equations involves solving for variables that satisfy multiple equations simultaneously.

Methods to Solve Systems

1. Substitution Method: Solve one equation for a variable and substitute it into the other. Example: \[ \begin{cases} y = 2x + 1\\ y = x - 3 \end{cases} \] Substituting \(y = 2x + 1\) into \(y = x - 3\):

   \(2x + 1 = x - 3 \implies x = -4, \quad y = -7\)

2. Elimination Method: Add or subtract equations to eliminate one variable. Example: \(2x + y = 5, \quad x - y = 3\) \[ \begin{cases} 2x + y = 5\\ x - y = 3 \end{cases} \] Add the equations: \(3x = 8 \implies x = \frac{8}{3}, y = \frac{1}{3}\)

3. Graphing Method: Plot both equations on a graph and find their intersection.

   • Note: This method may be unreliable for non-linear equations.

Special Cases

• No solution: Lines are parallel and never intersect.
• Infinite solutions: Equations represent the same line.

Example of No Solution

\[ \begin{cases} y = 2x + 1\\ y = 2x - 3 \end{cases} \] These lines are parallel and will not intersect.

---

Notation Tips

• Use | to mean “such that”. Example: \(\{x | x > 0\}\).
• Be clear about assumptions, such as domains and ranges for functions.

---

Thank you for visiting! Explore the other pages for more insights and resources.